Ejercicio 5.25. Estudio de los movimientos oscilatorios
 El estudio de los movimientos oscilatorios siempre ha sido motivo de conflicto, sobre todo para los alumnos. ¿Cuál es ese conflicto? En los cursos de Mecánica, hasta el estudio de los osciladores, se ven sistemas cuyo mayor grado de complejidad se da en casos con valores de aceleración constante. A partir de allí, dicha variable cinemática también cambia su valor en función del tiempo, lo que ocasiona en los alumnos cierto desconcierto. Desconcierto que aumenta cuando resuelven las ecuaciones diferenciales para hallar las variables cinemáticas (posición, velocidad y aceleración) y / o las variables dinámicas (cantidad de movimiento y fuerza), y pierden la capacidad de análisis del comportamiento del sistema desde el punto de vista físico, sobre todo cuando analizan el comportamiento de las variables que influyen - o no - en los citados movimientos.
Para tratar de solucionar esta situación, se propone una alternativa de estudio de los distintos Osciladores, utilizando la Dinámica de Sistemas como herramienta.
El Movimiento Oscilatorio Forzado
Se va a analizar el movimiento oscilatorio en una dimensión, que describe un sistema formado por un péndulo de resorte - un cuerpo de masa m, suspendido del extremo de un resorte ideal de constante elástica k -, cuando se lo perturba -se estira, o se comprime- respecto de su posición de equilibrio x0, una distancia x. El modelo puede utilizarse para analizar las variables cinemáticas (posición, velocidad y aceleración), o dinámicas (cantidad de movimiento y fuerza).
Si bien se pueden analizar las variables en forma individual, se agrupan en dos gráficos: uno que involucra las cinemáticas, y otro para cantidad de movimiento y fuerza. Incluso tiene una ventaja adicional: se puede analizar si existe movimiento oscilatorio amortiguado. ¿Cómo se hace? Simplemente, cambiando el valor de la constante de amortiguamiento b, y realizando la simulación. El siguiente gráfico nos lo muestra.
Si al modelo del oscilador amortiguado se le da el valor de b = 0, se tendrá un movimiento oscilatorio armónico. Esto muestra claramente de la gran utilidad educativa que tiene la Dinámica de Sistemas. Cambiando los valores de las variables que influyen en el movimiento, se puede analizar cómo se comporta el mismo. Por ejemplo, para el oscilador armónico simple, se puede vislumbrar el cambio en la amplitud, la longitud de onda, y la frecuencia (o el período, que es su recíproco) cuando se cambian los valores de k ó m en el modelo.
Conclusiones
Podemos obtener del modelo creado las conclusiones siguientes:
- Cuando aumenta la masa, aumenta el período del movimiento oscilatorio armónico;
El estudio de los movimientos oscilatorios siempre ha sido motivo de conflicto, sobre todo para los alumnos. ¿Cuál es ese conflicto? En los cursos de Mecánica, hasta el estudio de los osciladores, se ven sistemas cuyo mayor grado de complejidad se da en casos con valores de aceleración constante. A partir de allí, dicha variable cinemática también cambia su valor en función del tiempo, lo que ocasiona en los alumnos cierto desconcierto. Desconcierto que aumenta cuando resuelven las ecuaciones diferenciales para hallar las variables cinemáticas (posición, velocidad y aceleración) y / o las variables dinámicas (cantidad de movimiento y fuerza), y pierden la capacidad de análisis del comportamiento del sistema desde el punto de vista físico, sobre todo cuando analizan el comportamiento de las variables que influyen - o no - en los citados movimientos.
Para tratar de solucionar esta situación, se propone una alternativa de estudio de los distintos Osciladores, utilizando la Dinámica de Sistemas como herramienta.
El Movimiento Oscilatorio Forzado
Se va a analizar el movimiento oscilatorio en una dimensión, que describe un sistema formado por un péndulo de resorte - un cuerpo de masa m, suspendido del extremo de un resorte ideal de constante elástica k -, cuando se lo perturba -se estira, o se comprime- respecto de su posición de equilibrio x0, una distancia x. El modelo puede utilizarse para analizar las variables cinemáticas (posición, velocidad y aceleración), o dinámicas (cantidad de movimiento y fuerza).
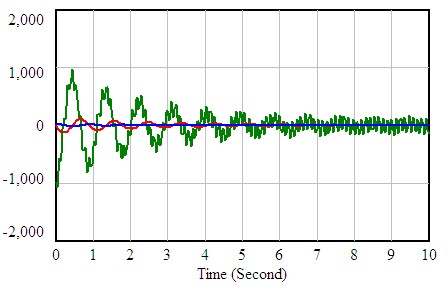
Si bien se pueden analizar las variables en forma individual, se agrupan en dos gráficos: uno que involucra las cinemáticas, y otro para cantidad de movimiento y fuerza. Incluso tiene una ventaja adicional: se puede analizar si existe movimiento oscilatorio amortiguado. ¿Cómo se hace? Simplemente, cambiando el valor de la constante de amortiguamiento b, y realizando la simulación. El siguiente gráfico nos lo muestra.
Si al modelo del oscilador amortiguado se le da el valor de b = 0, se tendrá un movimiento oscilatorio armónico. Esto muestra claramente de la gran utilidad educativa que tiene la Dinámica de Sistemas. Cambiando los valores de las variables que influyen en el movimiento, se puede analizar cómo se comporta el mismo. Por ejemplo, para el oscilador armónico simple, se puede vislumbrar el cambio en la amplitud, la longitud de onda, y la frecuencia (o el período, que es su recíproco) cuando se cambian los valores de k ó m en el modelo.
Conclusiones
Podemos obtener del modelo creado las conclusiones siguientes:
- Cuando aumenta la masa, aumenta el período del movimiento oscilatorio armónico;
- Cuando aumenta la constante k, disminuye el período del citado movimiento .
En consecuencia, existe una relación directa entre el período de oscilación y la masa del péndulo de resorte, e inversa entre dicho período y la constante elástica del resorte. En consecuencia, se podría escribir:
T = m / k
La expresión matemática del período en función de la masa y de la constante elástica del resorte, se puede hallar mediante el procesamiento de los datos numéricos de la simulación, o a través de las ecuaciones diferenciales que resultan de la aplicación de la segunda ley de Newton.
Mediante este trabajo se ha intentado explicar el gran aprovechamiento educativo que se puede hacer usando la Dinámica de Sistemas para el análisis de los Movimientos Oscilatorios Forzado, Amortiguado y Armónico.
Empleando el mismo modelo, y modificando los valores de las variables según el caso a estudiar, se obtienen gráficas que facilitan enormemente el análisis, la comprensión y la discusión del sistema analizado.
|

 Información
Información




 Información
Información


