Cadenas de Markov
Basado en un modelo de simulación con Vensim
Mario Guido Pérez
mariogperez@arnet.com.ar
Existen diferentes fenómenos, muchos de ellos en el campo social, que presentan una evolución temporal tal que permite modelarlos según un proceso de Markov.
Un proceso de Markov es una serie de experimentos en que cada uno tiene m posibles resultados, E1, E2.....Em, y la probabilidad de cada resultado depende exclusivamente del que se haya obtenido en los experimentos previos.
Por ejemplo: si en el mercado hay tres marcas de detergentes, cada una de las cuales tiene una cierta porción de dicho mercado en la semana 1, la semana siguiente la distribución puede cambiar dependiendo de las decisiones del consumidor (seguir con la misma marca o cambiar por otra), y esta decisión depende mucho de la última compra. Muchas otras situaciones presentan este patrón de comportamiento: los valores de las acciones de la bolsa día a día, la distribución de la población entre diferentes regiones año a año etc.
Matemáticamente, un proceso de Markov se modela mediante una matriz de transición.
Esta no es más que una matriz de probabilidades, donde cada elemento pij representa la probabilidad condicional de que el sistema pase de un estado actual i al siguiente estado j.
La resolución matemática tradicional es tediosa, puesto que si se quiere ver la evolución a lo largo de un cierto número de períodos, será necesario repetir operaciones matriciales tantas veces como períodos se quiera analizar.
Se ha aplicado una resolución utilizando las posibilidades que brinda la dinámica de sistemas, que además permite visualizar mejor el fenómeno, e incluir otros elementos adicionales al fenómeno en estudio.
EL MODELO
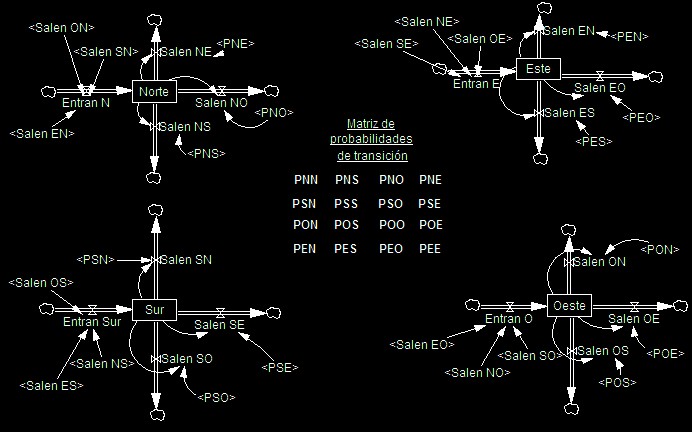
El modelo supone cuatro regiones dentro de una cierta zona en estudio, Norte, Sur, Este y Oeste, entre las cuales se producen migraciones cruzadas, habiéndose estudiado para cada región la probabilidad característica de que una persona permanezca en el lugar o se traslade a uno de los otros tres. Estas probabilidades se resumen en una Matriz de probabilidades de transición, donde cada elemento representa la probabilidad de que un poblador de una región pase a otra: así por ejemplo, PNS indica la probabilidad de que un poblador del Norte se mude al Sur. Puede verse que los elementos de la diagonal, indican las probabilidades de que permanezcan en la región de origen.
Cada nivel, Norte, Sur, Este y Oeste,disminuye según los flujos a otras regiones, y crece en base a los pobladores que recibe.
El modelo exhibe un comportamiento típico, puesto que a medida que avanza el tiempo tiende a un estado de equilibrio, en el cual las variaciones de población de cada región son casi nulas.
Adaptando los nombres de las variables, y extendiendo o disminuyendo del número de niveles y la matriz de transición, el modelo es aplicable a muy diversas situaciones.
Según Wikipedia la dinámica de sistemas es una técnica para analizar y modelar el comportamiento temporal en entornos complejos. Se basa en la identificación de los bucles de realimentación entre los elementos, y también en las demoras en la información y materiales dentro del sistema. Lo que hace diferente este enfoque de otros usados para estudiar sistemas complejos es el análisis de los efectos de los bucles o ciclos de realimentación, en términos de flujos y depósitos adyacentes. De esta manera se puede estructurar a través de modelos matemáticos la dinámica del comportamiento de estos sistemas. La simulación de estos modelos actualmente se puede realizar con ayuda de programas computacionales específicos.
Originalmente desarrollada en 1950 para ayudar a los administradores de empresas a mejorar su comprensión de los procesos industriales, actualmente se usa en el sector público y privado para el análisis y diseño de políticas. Fue creada a principios en la década de 1960 por Jay Forrester de la MIT Sloan School of Management del Massachusetts Institute of Technology) con la creación del MIT System Dynamics Group.
Los modelos de simulación con Dinámica de Sistemas tienen aplicaciones en prácticamente todas las áreas del conocimiento como podemos observar en los numerosos artículos publicados en los congresos anuales de la System Dynamics Society. Se trata de una potente herramienta para:
Enseñar a los reflejos del sistema de pensamiento de las personas que está siendo entrenado.
Analizar y comparar los supuestos y modelos mentales acerca de cómo funcionan las cosas.
Obtener una visión cualitativa sobre el funcionamiento de un sistema o las consecuencias de una decisión.
Reconocer arquetipos de sistemas disfuncionales en la práctica diaria.
Los modelos permiten simular el impacto de diferentes políticas relativas a la situación a estudiar ejecutando simulaciones what if (¿qué pasaría si?) que permiten ver las consecuencias a corto y medio plazo, y ser de gran ayuda en la comprensión de cómo los cambios en un sistema lo afectan en el tiempo. En este sentido es muy similar al Pensamiento sistémico ya que se basa en los mismos diagramas de causales con bucles o lazos de retroalimentación (feedback). Sin embargo, estos modelos de simulación permiten además hacer simulaciones para estudiar el comportamiento de los sistemas y el impacto de políticas alternativas. Se utiliza en especial para investigar la dependencia de los recursos naturales y los problemas resultantes del creciente consumo a nivel global para mejorar el especial en el desarrollo de nuevos productos. Existe una gran variedad de marcas de software en el mercado que ayudan a aplicar esta herramienta de una forma amigable: Vensim, Stella, ithink, Powersim, Dynamo, etc.
(*) Puede solicitar información más detallada de este trabajo al autor
|













